by Alyssa Ladwig
and Jon Luetke
Being able to understand the electronic structure of a molecule allows one to determine the reactivity of the molecule. It also allows one to predict the locations of the electrons, vibrational frequencies, potential energy, and the UV-Visible transitions. These properties are useful to determine whether a molecule will react in a reaction or not. To find these properties, wavefunctions for the electrons are formulated. The expectation value of energy is calculated by taking the integral of the wavefunction multiplied by the Hamiltonian operator and the conjugated wavefunction. The calculations are complicated and require computer technology. For the purposes of this experiment, the computer program GAMESS was used to calculate the integrals. Two methods of calculations were used, MOPAC and ab initio. Ab initio is the best level of theory. It calculates all the integrals, but the calculations can be lengthy depending upon the molecule. From these calculations, diagrams of the highest occupied molecular orbital (HOMO) and potential energy curves were created and information about the vibrational frequencies and UV-Visible transitions were collected for the molecules fluorine (F2), carbon monoxide (CO), and para-dibromobenzene (C6H4Br2).
The optimized geometry for each molecule was essential to determine before completing any additional calculations. The ideal geometry was chosen by comparing the calculated values for bond lengths with the literature values. The basis set with the closest bond length was chosen. For fluorine, the 631Gd calculated value for the bond length of 1.412529 Aº was closest to the literature value of 1.4119 Aº. For carbon monoxide, the 321G calculated value for the bond length of 1.128936 Aº was closest to the literature value of 1.1283 Aº. The literature values were obtained from the NIST Computational Chemistry Comparison and Benchmark Database.
Fluorine Optimized Geometry Carbon Monoxide Optimized Geometry

The calculated bonds for each of the levels of theory were compared to the literature values for para-dibromobenzene. The double zeta calculation proved to be the closest to the literature values (Table 1).
Para-dibromobenzene Optimized Geometry
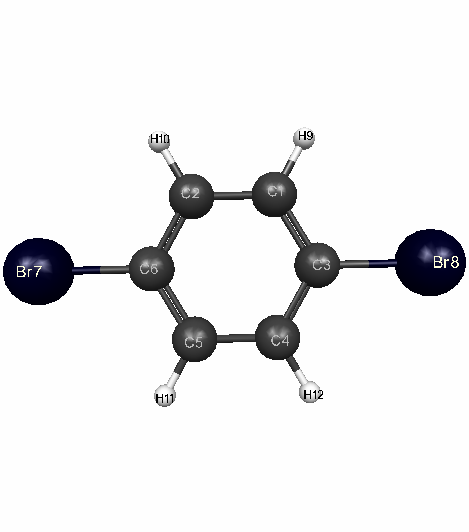
Table 1: Para-dibromobenzene Optimized
Bond Lengths for Double Zeta Basis Set
| Bond | Calculated Values (Aº) | Literature Values (Aº) |
| Br-C1 |
1.89344 |
1.906 |
| C1-C2 |
1.38854 |
1.388 |
| C2-C3 |
1.39236 |
1.394 |
| C-H |
1.0714 |
1.09 |
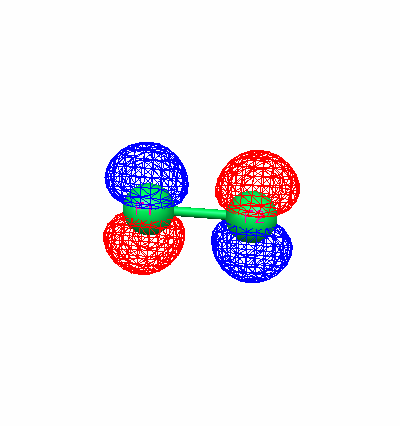
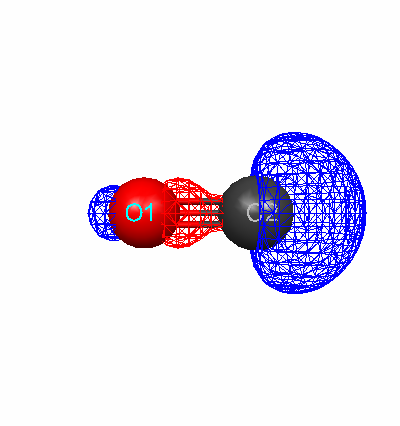
Using the optimized geometry, diagrams of the highest occupied molecular orbital (HOMO) were created for each molecule.
Fluorine HOMO (Energy Level 9) Carbon monoxide HOMO (Energy Level 7)
Para-dibromobenzene HOMO (Energy Level 55)

The potential energy surface as a
function of bond length was calculated for the diatomic molecules at
each level of ab initio
theory. At higher levels of theory (more complex) the potential
energy values decreased. Comparing the two diatomic molecules,
fluorine had a much more negative potential energy than carbon monoxide
overall. When comparing both diatomics it can be seen that there
is a potential well in each where the minimal value is near the
equilibrium bond length.
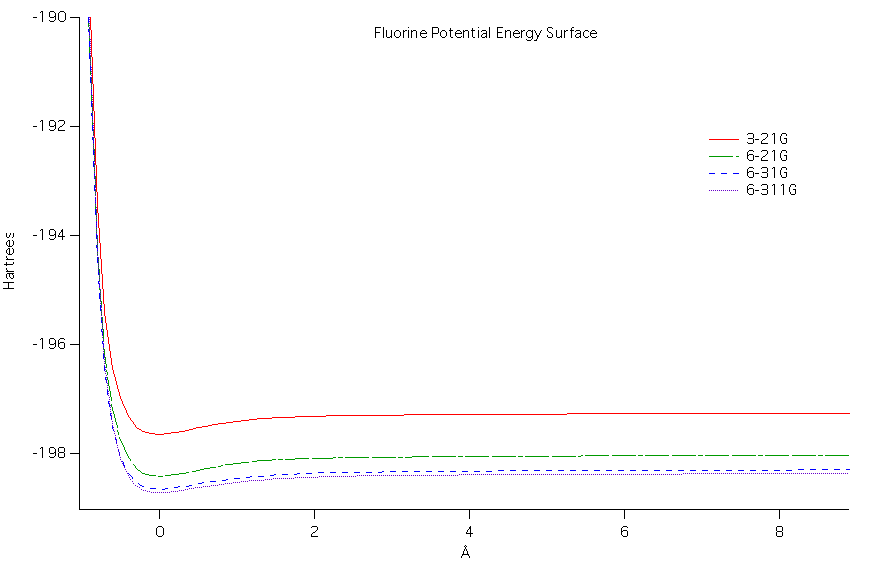
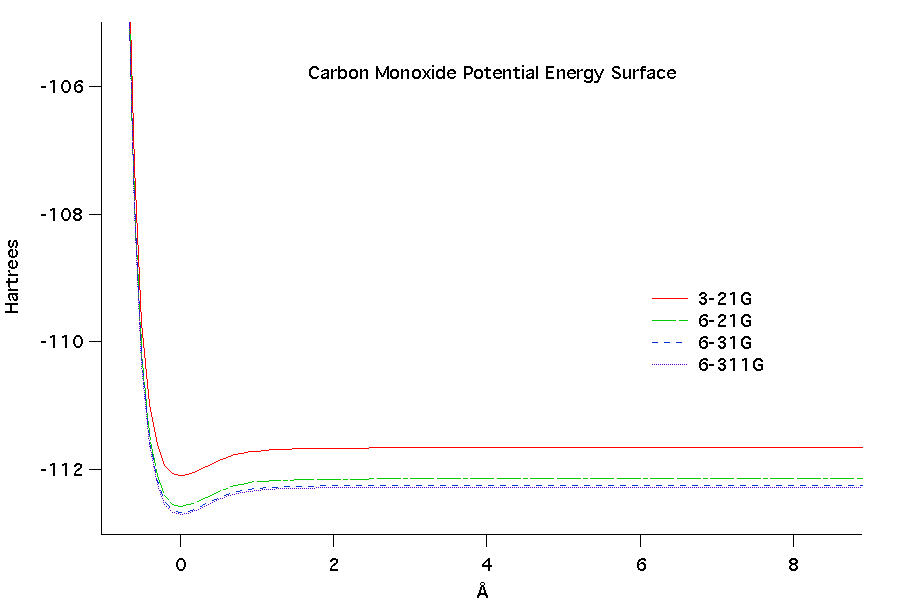


The vibrational frequencies for the
three molecules were calculated using the optimized geometry.
Table 2: Diatomic Molecule Frequency Data
The literature values were obtained from the NIST Computational
Chemistry Comparison and Benchmark Database.
Table 3: Para-dibromobenzene Frequency Data (cm-1)
A comparison to the literature values for the para-dibromobenzene is most effectively accomplished by comparing the calculated results to a literature Infared spectrum. The NIST website can be used to make such a comparison: http://webbook.nist.gov/cgi/cbook.cgi?ID=C106376&Units=SI&Type=IR-SPEC&Index=1#IR-SPEC
As can be seen, the calculated vibrational frequency for fluorine is well outside any range of error for the literature value. Carbon monoxide is closer to the literature value, however still quite different. When comparing the calculated values to the IR spectrum of para-dibromobenzene, a large number of the calculated values cannot be seen on the spectrum. Therefore, the accuracy of any values less than 400cm-1 cannot be determined. The calculated values over 3000cm-1 are not shown as peaks in this region represented on the spectrum.
When considering the representative motion of the significant peaks in the para-dibromobenzene spectrum the following motions are represented.
Table 4: Relative Motions for Significant Peaks in the Calculated Vibrational Frequencies for Para-dibromobenzene
The values for transition energy of an electron from the ground state to an excited state were calculated for para-dibromobenzene for the 3-21G and 6-31G basis sets. The calculated data can be seen in the following tables. In addition to the value for transition energy, a value for oscillator strength is also given. This oscillator strength can be used to determine the strength of the peak that would be displayed on a UV-Visible spectrum.
Table 5: Para-dibromobenzene UV-Visible Results for 3-21G Basis Set
Table 6: Para-dibromobenzene UV-Visible Results for 6-31G Basis Set
Table 2: Diatomic Molecule Frequency Data
| Molecule |
Calculated
Frequency (cm-1) |
Literature
Values (cm-1) |
| F2 |
1141.609985 |
916.6 |
| CO |
2312.689941 |
2169.8 |
Table 3: Para-dibromobenzene Frequency Data (cm-1)
| 95.389999 |
479.970001 |
1082.750000 |
1213.290039 |
1752.900024 |
| 162.570007 |
602.950012 |
1106.609985 |
1314.989990 |
1787.920044 |
| 231.279999 |
696.559998 |
1173.420044 |
1325.780029 |
3402.360107 |
| 309.390015 |
763.799988 |
1175.619995 |
1446.219971 |
3422.179932 |
| 350.869995 |
867.400024 |
1197.609985 |
1533.069946 |
3429.979980 |
| 465.910004 |
1027.540039 |
1201.030029 |
1655.630005 |
3448.949951 |
A comparison to the literature values for the para-dibromobenzene is most effectively accomplished by comparing the calculated results to a literature Infared spectrum. The NIST website can be used to make such a comparison: http://webbook.nist.gov/cgi/cbook.cgi?ID=C106376&Units=SI&Type=IR-SPEC&Index=1#IR-SPEC
As can be seen, the calculated vibrational frequency for fluorine is well outside any range of error for the literature value. Carbon monoxide is closer to the literature value, however still quite different. When comparing the calculated values to the IR spectrum of para-dibromobenzene, a large number of the calculated values cannot be seen on the spectrum. Therefore, the accuracy of any values less than 400cm-1 cannot be determined. The calculated values over 3000cm-1 are not shown as peaks in this region represented on the spectrum.
When considering the representative motion of the significant peaks in the para-dibromobenzene spectrum the following motions are represented.
Table 4: Relative Motions for Significant Peaks in the Calculated Vibrational Frequencies for Para-dibromobenzene
| Frequency (cm-1) |
Description of Motion |
| 465.910004 |
sliding of benzene ring between
bromines |
| 602.950012 |
folding of molecule around axis
running through bromines |
| 1082.750000 |
flapping motion of carbons with
hydrogens attached |
| 1106.609985 |
anti-symmetric planar stretch of
carbons with hydrogens attached |
| 1201.030029 |
anti-symmetric stretching
between C2, C6 and C3, C4 |
| 1533.069946 |
anti-symmetric planar stretch
between C1, C2 and C4, C5 |
| 1655.630005 |
symmetric planar stretches of C1
and C4 from C3 |
| 3448.949951 |
stretching between hydrogen and
carbon on benzene ring |
The values for transition energy of an electron from the ground state to an excited state were calculated for para-dibromobenzene for the 3-21G and 6-31G basis sets. The calculated data can be seen in the following tables. In addition to the value for transition energy, a value for oscillator strength is also given. This oscillator strength can be used to determine the strength of the peak that would be displayed on a UV-Visible spectrum.
Table 5: Para-dibromobenzene UV-Visible Results for 3-21G Basis Set
| From Ground
State to Excited State |
Transition
Energy (cm-1) |
Oscillator
Strength |
| 1 |
51427.24 |
0.001407 |
| 2 |
52826.77 |
0.137390 |
| 3 |
55333.80 |
0.000000 |
| 4 |
56997.53 |
0.014225 |
| 5 |
64074.29 |
0.006629 |
| 6 |
64198.74 |
0.000000 |
| 7 |
67217.40 |
1.653998
(Primary) |
| 8 |
68624.24 |
0.876194
(Secondary) |
| 9 |
70255.07 |
0.000000 |
| 10 |
74088.20 |
0.000000 |
Table 6: Para-dibromobenzene UV-Visible Results for 6-31G Basis Set
| From Ground
State to Excited State |
Transition
Energy (cm-1) |
Oscillator
Strength |
| 1 |
50824.08 |
0.000274 |
| 2 |
52116.67 |
0.116610 |
| 3 |
54799.24 |
0.000000 |
| 4 |
56446.28 |
0.010258 |
| 5 |
64607.43 |
0.004443 |
| 6 |
64721.19 |
0.000000 |
| 7 |
66374.97 |
1.727890
(Primary) |
| 8 |
67719.53 |
0.902194
(Secondary) |
| 9 |
68290.52 |
0.000000 |
| 10 |
73855.20 |
0.000000 |
From the vibrational frequency and transition energy calculations, it can be seen that their ab initio calculations were not good predictors of literature values. The bond length calculations used to determine the optimized geometry were very close to literature values. Therefore, ab initio could be used to optimize molecules but would not be accurate in predicting vibrational frequencies and transition energies.